基于后缀算术表达式的代码解析
三月 18, 2021引子
最近在设计一个数据字段的运算表达式控件，具体不废话，可以参看下面的动画截图：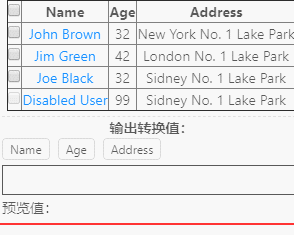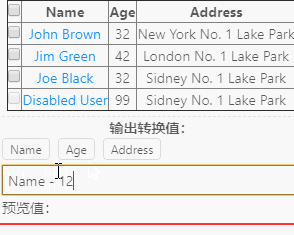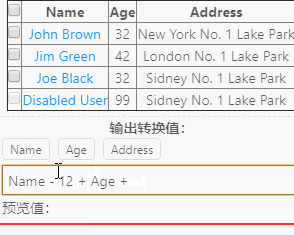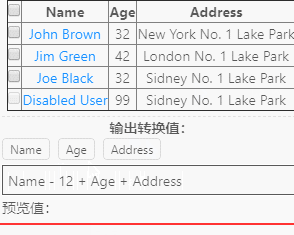
截图里有一个表格内容数据(是程序运行时从其他外部网页抓取的数据)，而我需要根据表格的属性字段去做对应的算术运算，如（加减乘除）或者(一些函数命令)
然后则根据表达式解析计算出对应的结果，需求就是这样的。
思路
具体实现借用了 入栈的想法，将字符串分割出对应的运算符、值、函数表达式，我这里使用了mapping关系来处理，将整个字符串里的 运算符和函数表达式 替换出对应的空值加key的形式：
// 我的运算符和函数mapping表
const operationOptions = [
{
label: "取长度",
call: "取长度",
weight: 10,
},
{
label: "转大写",
call: "转大写",
weight: 10,
},
{
label: "转小写",
call: "转小写",
weight: 10,
},
{
label: "-",
call: "-",
weight: 1,
},
{
label: "+",
call: "+",
weight: 1,
},
{
label: "/",
call: "/",
weight: 2,
},
{
label: "*",
call: "*",
weight: 2,
},
{
label: "(",
call: "(",
weight: 9,
},
{
label: ")",
call: ")",
weight: 9,
},
{
label: "（",
call: "(",
weight: 9,
},
{
label: "）",
call: ")",
weight: 9,
},
]
// 中缀表达式
const converToInfix = (str) => {
let newStr = str;
operationOptions.forEach(c => {
newStr = newStr.replace(new RegExp(`\\${c.label}`, "gi"), " " + c.call + " ");
});
return newStr.split(/\s/).filter(c => c);
}返回得到的是被分割好的关键字代码数组，还是中缀表达式
得到关键字代码数组后，对于程序计算这个时候还是不太方便，所以我这边还将中缀表达式转换为了后缀表达式, 中缀表达式转后缀表达式的转换思想如下：
// 1、需遍历整个字符串
// 2、开辟一个临时栈区，用数组表示即可，再开辟一个后缀表达式存储区
// 如 const suffixArr = [];
// const stack = [];
// 遍历时, 如果遇到数值类型 则直接压入 suffixArr
// 比如遇到 3，则压入suffixArr，此时为：suffixArr = [3];
// 如果遇到运算符（+-*/）等或者函数表达式，则需关注stack的存储：
// 如果当前的运算符权重比stack中的栈顶（也就是最后一位）运算符权重小，
// 则需要将栈顶出栈，然后放入到suffixArr后面
// 接着继续比较当前的栈顶权重是否大于等于当前的运算符权重，如果大于等于，则继续出栈，放入到suffixArr后
// 直到当前的栈顶不存在或者权重小于当前运算符权重
// 最后把当前运算符加入到stack中
// 如果当前的运算符权重比stack中栈顶运算符权重大，则直接将此运算符入栈stack
//
// 如果遇到“(” 运算符
// 则直接入栈stack
// 如果遇到“)” 运算符
// 则需在stack中出栈到最近的一个“(”运算符，出栈的运算符都加到suffixArr后
// 如果出栈到最近的一个“(”运算符后，发现此时栈顶还是一个函数表达式，则还需将此表达式出栈到suffixArr中以 9 + 取长度(3 + 1 * (8 - 2) / 2) - 2 * 3 + 7 为例：
有 suffixArr = [] 和 stack = []第1步：遇到数值 9, 加入到suffixArr中，此时 suffixArr = [9]; stack = [];
第2步: 遇到运算符 +, 加入到stack中，此时 suffixArr = [9]; stack = [+];
第3步: 遇到函数表达式 取长度, 加入到stack中，此时 suffixArr = [9]; stack = [+, 取长度];
第4步: 遇到优先级符号 (, 加入到栈中，此时 suffixArr = [9]; stack = [+, 取长度, (];
第5步: 遇到数值 3, 加入到suffixArr中，此时 suffixArr = [9, 3]; stack = [+, 取长度, (];
第6步: 遇到运算符 +, 因为此时的栈顶为(，不需要比较权重，则入栈，此时 suffixArr = [9, 3]; stack = [+, 取长度, (, +];
第7步: 遇到数值 1, 加入到suffixArr中，此时 suffixArr = [9, 3, 1]; stack = [+, 取长度, (, +];
第8步: 遇到运算符 , 因为在mapping中定义的的权重大于+，所以，当前stack的栈顶+比的权重小，所以不用出栈，则直接入栈，此时 suffixArr = [9, 3, 1]; stack = [+, 取长度, (, +, ];
第9步: 遇到优先级符号 (, 加入到栈中，此时 suffixArr = [9, 3, 1]; stack = [+, 取长度, (, +, , (];
第9步: 遇到数值 8, 加入到suffixArr中，此时 suffixArr = [9, 3, 1, 8]; stack = [+, 取长度, (, +, , (];
第10步: 遇到运算符 -, 因为此时的栈定为(，不需要比较权重，则入栈，此时 suffixArr = [9, 3, 1, 8]; stack = [+, 取长度, (, +, , (, -];
第11步: 遇到数值 2, 加入到suffixArr中，此时 suffixArr = [9, 3, 1, 8, 2]; stack = [+, 取长度, (, +, , (, -];
第12步: 遇到优先级符号 ), 则需要将stack中从栈定依次出栈到最近的一个 “(“ 符号, 并加入到suffixArr后面，”(“ 符号不加入，此时 suffixArr = [9, 3, 1, 8, 2, -]; stack = [+, 取长度, (, +, ];
第13步: 遇到运算符 /, 因为此时栈顶为，和/的权重一样，所以入栈，此时 suffixArr = [9, 3, 1, 8, 2, -]; stack = [+, 取长度, (, +, , /];
第14步: 遇到数值 2, 加入到suffixArr中，此时 suffixArr = [9, 3, 1, 8, 2, -, 2]; stack = [+, 取长度, (, +, , /];
第15步: 遇到优先级符号 ), 则需要将stack中从栈定依次出栈到最近的一个 “(“ 符号, 并加入到suffixArr后面，”(“ 符号不加入，此时 suffixArr = [9, 3, 1, 8, 2, -, 2, /, , +]; stack = [+, 取长度]; 因为找到最近一个“(”后，当前的栈顶为取长度是函数表达式, 则需要出栈加入到suffixArr后，则此时，suffixArr = [9, 3, 1, 8, 2, -, 2, /, , +, 取长度]; stack = [+]
第16步: 遇到运算符 -, 因为此时的栈定为+，权重和-是一样的，则直接入栈，此时 suffixArr = [9, 3, 1, 8, 2, -, 2, /, , +, 取长度]; stack = [+, -];
第17步: 遇到数值 2, 加入到suffixArr中，此时 suffixArr = [9, 3, 1, 8, 2, -, 2, /, , +, 取长度, 2]; stack = [+, -];
第18步: 遇到运算符 , 因为此时的栈定为-，权重比栈顶大，则直接入栈，此时 suffixArr = [9, 3, 1, 8, 2, -, 2, /, , +, 取长度, 2]; stack = [+, -, ];
第19步: 遇到数值 3, 加入到suffixArr中，此时 suffixArr = [9, 3, 1, 8, 2, -, 2, /, , +, 取长度, 2, 3]; stack = [+, -, ];
第20步: 遇到运算符 +, 因为此时的栈顶为，权重比栈顶小，则栈顶需出栈后加入到suffixArr中，此时 suffixArr = [9, 3, 1, 8, 2, -, 2, /, , +, 取长度, 2, 3, ]; stack = [+, -]; 出栈后，需要再此查看接下来的当前stack中栈顶的权重是否大于等于此时的运算符+权重，如果权重大于等于此时的运算符+, 则依次出栈加入到suffixArr中，直到栈顶小于此时运算符的权重，则此时结果：suffixArr = [9, 3, 1, 8, 2, -, 2, /, , +, 取长度, 2, 3, , -, +]; stack = []; 出栈完后，则需要将此时的运算符+压栈到stack中，则此时 uffixArr = [9, 3, 1, 8, 2, -, 2, /, , +, 取长度, 2, 3, , -, +]; stack = [+];
第21步: 遇到数值 7, 加入到suffixArr中，此时：suffixArr = [9, 3, 1, 8, 2, -, 2, /, , +, 取长度, 2, 3, , -, +, 7]; stack = [+];
第22步：依次出栈stack加入到suffixArr中，则此时 suffixArr = [9, 3, 1, 8, 2, -, 2, /, , +, 取长度, 2, 3, , -, +, 7, +]; stack = [];
则最后的后缀表达式为: 9 3 1 8 2 - 2 / * + 取长度 2 3 * - + 7 +;
代码实现如下：
const converToSuffix = (str) => {
const infixStrArr = converToInfix(str);
const suffixArr = [];
const stack = [];
// 判断括号是否匹配
let leftBracketLen = 0;
let rightBracketLen = 0;
let stackTop;
infixStrArr.map(c => {
const values = operationOptions.map(d => d.call).filter(d => d !== "(" && d !== ")");
if (values.includes(c)) {
// 需要判断栈顶的的权重是否比需要入栈的权重大
// 如果栈顶权重比较大则需弹出
// 弹出后检查比当前op还大于等于的操作
// 最后弹出后再将op入栈
const op = operationOptions.find(d => d.call === c);
if (stack.length) {
stackTop = stack[stack.length - 1];
}
// 第一次判断
if (stackTop && stackTop.weight > op.weight && stackTop.weight < 9) {
// 出栈后继续判断
suffixArr.push(stack.pop());
stackTop = stack[stack.length - 1] || null;
while (stackTop && stackTop.weight >= op.weight && stackTop.weight < 9) {
suffixArr.push(stack.pop());
stackTop = stack[stack.length - 1] || null;
}
}
stack.push(op);
return;
}
if (c === ")") {
rightBracketLen++;
// 遇到右括号 则出栈对应的操作符到左括号
stackTop = stack.pop();
while (stackTop && stackTop.call !== "(") {
suffixArr.push(stackTop);
stackTop = stack.pop() || null;
}
// 判断是否自定义的func
let lastStackTop = stack.length - 1;
if (stack[lastStackTop] && stack[lastStackTop].weight >= 10) {
suffixArr.push(stack.pop());
lastStackTop = stack.length - 1;
stackTop = stack[lastStackTop] || null;
}
return;
}
if (c === "(") {
leftBracketLen++;
stackTop = operationOptions.find(d => d.call === '(');
stack.push(stackTop);
return;
}
// console.log(c, stack);
suffixArr.push({call: c});
});
if (leftBracketLen !== rightBracketLen) {
throw new Error("操作运算符括号不匹配");
}
return [].concat(suffixArr.map(c => c.call), stack.reverse().map(c => c.call));
}解析
有了后缀表达式的转换后，我们最后只需要实现后缀表达式的遍历运算即可，见下面代码：
const calc = str => {
const suffixArr = converToSuffix(str);
const stack = [];
// 不需要有()运算符参与了
const operators = operationOptions.map(c => c.call).filter(c => c !== "(" && c !== ")");
suffixArr.forEach(c => {
if (operators.includes(c)) {
stack.push(
withOperation(stack, c)
)
} else {
stack.push(withData(c));
}
})
return stack.pop();
};
const withData = c => {
const globalData = typeof window === "undefined" ? global : window;
const data = globalData[String(c)] || null;
if (data) {
return data;
}
if (isNaN(Number(c))) {
return String(c);
}
return Number(c);
};
const withOperation = (stack, type) => {
let result;
switch(type) {
case "+": {
result = withData(stack.pop()) + withData(stack.pop());
break;
}
case "-": {
const rightValue = stack.pop();
const leftValue = stack.pop();
result = withData(leftValue) - withData(rightValue);
break;
}
case "*": {
result = withData(stack.pop()) * withData(stack.pop());
break;
}
case "/": {
const rightValue = stack.pop();
const leftValue = stack.pop();
result = withData(leftValue) / withData(rightValue);
break;
}
case "取长度": {
// 简单实现一个自定义的取长度功能
const value = withData(stack.pop());
result = new Array(Math.abs(value)).fill(0).length;
break;
}
default: {
break;
}
}
return result;
}最后执行测试一下：
global.ffa = 7;
const a = operation("9 + 取长度(3 + 1 * (8 - 2) / 2) - 2 * 3 + ffa");
console.log(a); // ---------> 16结尾
对于一些数组如 arr[0] 或者 person.say() 可以语法可以再思考一下