DDA算法

八月 13, 2018

直线段的扫面转换算法

数学上，直线上的点有无穷多个。但当在计算机光栅显示器屏幕上表示这条直线时需要做一些处理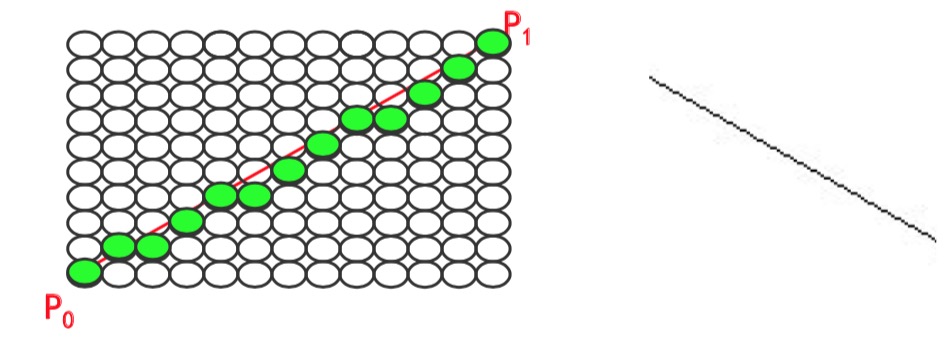

为了在光栅显示器上用这些 离散的像素点逼近这条直 线，需要知道这些像素点的 x，y坐标。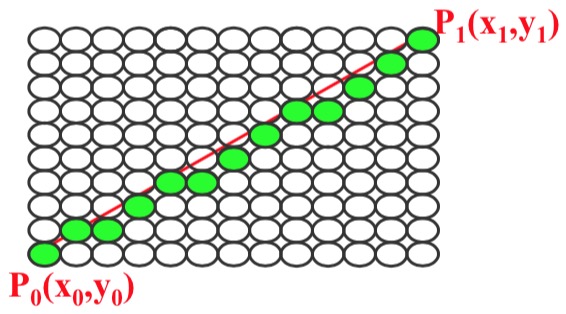

求出过p0,p1的直线段方程:

y = kx + b  
k = (y1 - y2) / (x1 - x2)   // (x1 != x2)

假设x已知，即从x的起点x0开始 ，沿x方向前进一个像素(步长 = 1)，可以计算出相应的y值。
因为像素的坐标是整数，所以y值 还要进行取整处理
把数学上的一个点扫描转换一个屏幕像素点

如:
p(1.7，0.8) ->取整 -> p(1, 0)
p(1.7, 0.8) -> (+0.5) -> p(2.2, 1.3) ->取整 -> p(2, 1)

直线是最基本的图形，一个动画或真实感图形往往需要调用成千上万次画线程序，因此直线算法的好坏与效率将直接影响图形的质量和显示速度。
回顾下刚才的算法：
y = kx + b
计算机为了提高效率，把计算量减下来，选择一些算法把乘法取消了

DDA算法

引进图形学中一个很重要的思想—增量思想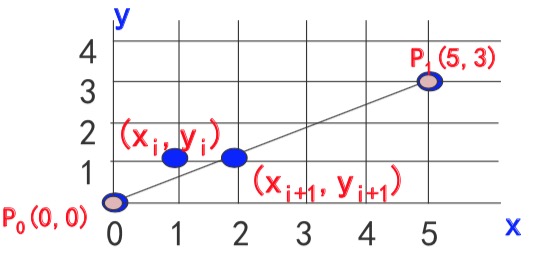
$$ y_i = kx_i + b $$ $$ y_{i+1} = kx_{i+1} + b $$ $$ =k(x_i + 1) +b $$ $$ =kx_i + k +b $$ $$ =y_i +b $$ $$ y_{i+1} = y_{i} + k $$

• 这个式子的含义是:当前步的y值等于前一步的y值 加上斜率k，这样就把原来一个乘法和加法变成了一个加法！

DDA算法演示例子

用DDA扫描转换连接两点P0(0,0)和P1(5,3)的直线段。画出线段如下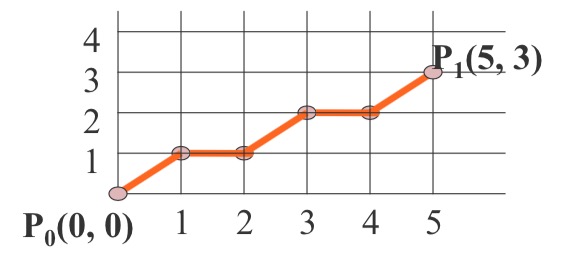： $$ k = \frac {y_1 - y_0}{x_1 - x_0} = \frac {3 - 0}{5 - 0} = 0.6 < 1 $$

x	y	int(y + 0.5) 取整
0	0	0
1	0+0.6	1
2	0.6+0.6	1
3	1.2+0.6	2
4	1.8+0.6	2
5	2.4+0.6	1

$$计算过程, 根据DDA增量算法: y_{i+1} = y_i + k
这里k = 0.6 $$

DDA不是最优

1、浮点数运算
2、限制在斜截式方程